Quadrato magico... particolare

Nella forma tradizionale, il quadrato magico è una matrice quadrata composta da numeri in modo che la somma di ciascuna riga, di ciascuna colonna e di ciascuna diagonale sia sempre uguale.
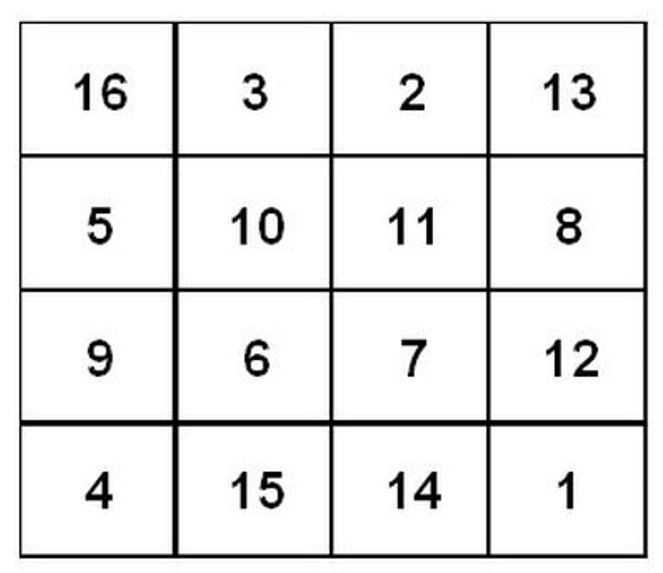
Un esempio, noto come quadrato di Durer, è il seguente:

La somma che resta invariata vale 34. Un’attività molto interessante da fare con gli alunni, consiste nello scoprire le diverse posizioni, oltre a quelle standard, di quaterne di numeri che soddisfino tale proprietà.

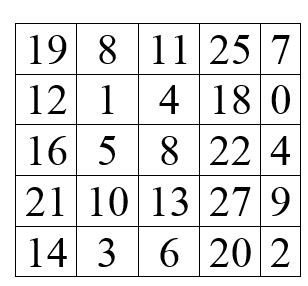
Il seguente quadrato, però, è del tutto diverso.

A prima vista sembra non avere una struttura sistematica: i numeri sembrano distribuiti nella matrice a caso; eppure possiede una proprietà magica…

Un modo per scoprire tale proprietà potrebbe essere questo.
Chiedete ad un alunno di scegliere un numero qualsiasi nel quadrato; cerchiatelo e cancellate tutti gli altri numeri nella stessa riga e nella stessa colonna; chiedete, ora, di scegliere un secondo numero tra quelli rimasti, eseguendo lo stesso procedimento; ripetendo il tutto per altre due volte rimarrà una sola casella scoperta: cerchiatela.
A questo punto, sommate i cinque numeri cerchiati, apparentemente scelti a caso, la loro somma sarà sicuramente 57. Non è un caso.

Il quadrato è una sorta di tabellina delle somme, generata da due insieme di numeri: 12,1,4,18 0 e 7, 0, 4, 9, 2. La somma di questi numeri è 57.
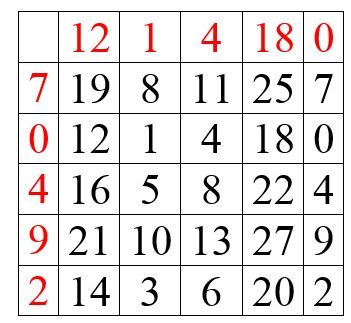
Scriviamo il primo insieme di numeri in orizzontale sopra la prima riga del quadrato e il secondo insieme in verticale a fianco della prima colonna:

Si nota subito come vengono determinati i numeri nelle varie caselle: il numero della prima casella, infatti, è la somma di 12 e 7, e così via.
Quindi il principio che sta alla base del “trucco” è il seguente: ogni numero nel quadrato rappresenta la somma di una coppia di numeri presenti nei due insiemi generatori. Quella particolare coppia viene eliminata, quando si cerchia il numero scelto. Il procedimento è tale per cui ogni scelta si trova in una colonna e in una riga diverse da tutte le altre, così che vengono selezionate le somme di cinque diverse coppie dei dieci numeri generatori, che equivalgono alla somma di tutti i dieci numeri.

È interessante e stimolante proporre ai ragazzi di provare a costruire un quadrato magico di questo tipo; non importa la dimensione e le combinazioni di numeri usati per generarlo: possono essere positivi o negativi, interi o frazionari, razionali o irrazionali.

Buon divertimento!