Polimini

Il termine polimino è stato introdotto da Solomon W. Golomd, matematico ricercatore, nel 1954. Egli lo definì un insieme di quadrati che abbiano a due a due un lato in comune.

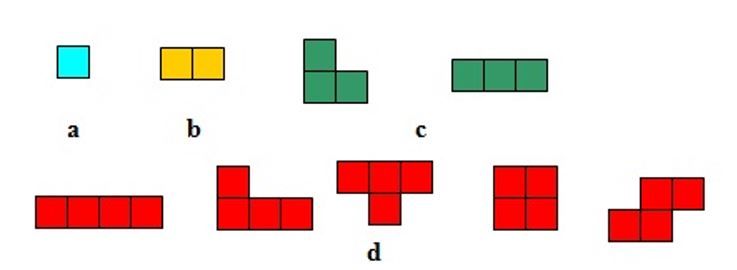
 Legenda: a) monomino, b) domino, c) trimino, d) tetramino.

Per ogni numero di quadrati considerati, si possono costruire diversi tipi di polimini.
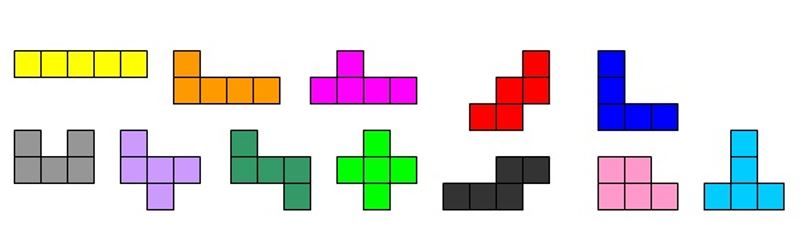
Infatti, esistono un solo tipo di domino, due trimini, cinque tetramini, dodici pentamini e così via; i pezzi asimmetrici, che hanno una forma diversa quando vengono “ribaltati”, sono considerati come un tipo unico.
Si può notare facilmente che il numero dei polimini distinti di qualsiasi ordine è in funzione del numero dei quadrati che li compongo, ma ancora nessuno è riuscito a trovare la formula che mette in relazione queste due grandezze.

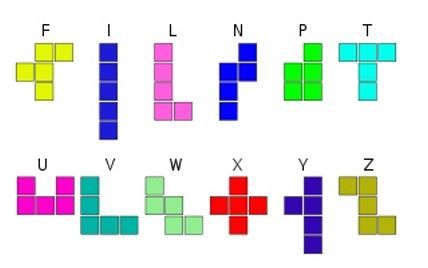
Consideriamo, ora, il gruppo dei 12 pentamini e vediamo come li possiamo utilizzare durante un’ora di matematica ricreativa.

Prima di giocare è utile costruire i dodici penatamini con quadratini di cartoncino o in legno e colorarli in modo diverso.

Per distinguerli meglio si possono associare alle lettere dell’alfabeto.

Tenendo presente che le lettere non sono simmetriche, occorre colorali su entrambe le facce, in modo che si possono appoggiare indifferentemente sull’una o sull’altra faccia.

Gioco 1

Sapendo che la superficie totale dei 12 pentamini è composta da 60 quadratini, 12 x 5 = 60, provare a costruire con essi i seguenti rettangoli in modi diversi:
4 x 15; 5 x 12; 6 x 10; 3 x 20 ( il più difficile).
Infine provare a costruire un quadrato. Cosa succede?

Gioco 2

Consideriamo una scacchiera 8 x 8.
Avendo a disposizione i 12 pentamini, due giocatori a turno ne scelgono uno e lo collocano a piacere sulla scacchiera. Perde il giocatore che non riesce più a collocare un pezzo senza che vada a sovrapporsi agli altri.

n.b. A riguardo, afferma Golomb, il gioco ha un minimo di 5 mosse, un massimo di 12 e non può mai finire alla pari.

Gioco 3 (Problema della triplicazione - Raphael Robinson)

Si seleziona un pentamino e poi si usano nove dei rimanenti per formare un modello in grande scala del pezzo scelto. Il modello sarà tre volte più alto e più largo del pezzo scelto. (Il problema può essere risolto per ciascuno dei 12 pezzi).

Gioco 4

Usare tutti i 12 pezzi per costruire un rettangolo 5 x 13 con un buco della forma di uno dei pezzi. (Si può risolvere con un buco della forma di qualsiasi pentamino).