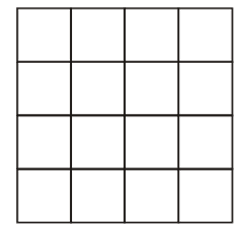
Sicuramente avrete già visto questa immagine seguita dalla domanda:
quanti quadrati riesci a contare nella figura?
Viene automatico iniziare a contare i quadrati con lato lungo 1, che sono 16, quelli con lato lungo 2, che sono 9, poi quelli con lato 3, che sono 4, infine l’ultimo quadratone di lato 4.
In tutto: 16 + 9 + 4 + 1 = 30.
Interessante è provare ad estendere il ragionamento e chiedersi: quanti quadrati ci sono in una scacchiera composta da n x n quadrati?
Riconsiderando la somma finale: 16 + 9 + 4 + 1 = 30 , notiamo che gli addendi sono i rispettivi quadrati dei numeri 1, 2, 3, 4 (lunghezza del quadrato grande).
Provando con una scacchiera 8 x 8, che si usa nel gioco degli scacchi, si ottiene:
8^2+7^2+6^2+5^2+4^2+3^2+2^2+1=204
Quindi, in quadrato n x n, il numero dei quadrati che si riescono a contare è dato dalla formula:
n^2+(n-1)^2+(n-2)^2+(n-3)^2+⋯+2^2+1^2