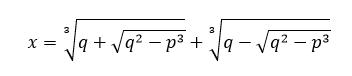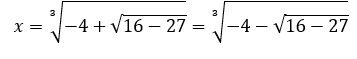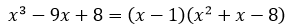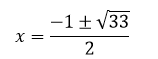Prima dell'unità i

 L’origine dei numeri complessi è collegata alla risoluzione delle equazioni di terzo grado. Consideriamo l’equazione:

la sua soluzione si trova utilizzando la formula di Cardano-Del Ferro:

Soffermando l’attenzione sulla quantità 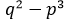, se essa è maggiore o uguale a zero permette di calcolare una soluzione dell’equazione mediante l’estrazione di radice, ma cosa succede se tale quantità è negativa?

Nell’equazione  in cui   si trova

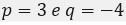
in cui compare la radice quadrata di un numero negativo.
Risolvendo la stessa equazione in modo esplicito si osserva che una radice è x = 1 e pertanto risulta:

Quindi le altre due radici si ottengono risolvendo l’equazione :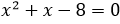

Arriviamo, dunque, ad una situazione paradossale, da una parte l’equazione ha tre soluzione reali, dall’altra la formula risolutiva non è in grado di darcene nemmeno una, a meno che non si dia un senso alle radici negative.

Si tratta del caso irriducibile dell’equazione di terzo grado, chiamato così perché la sua soluzione non può essere ricondotta semplicemente al calcolo di radicali, e che ha fatto discutere i matematici per più di due secoli.
Il primo che abbia tentato di dare un senso al caso irriducibile della formula di Gerolamo Cardano è il matematico Bombelli, nella sua opera Algebra del 1572.
Il suo tentativo prevede l’introduzione di due nuovi segni, oltre i classici + e -, che egli chiama più di meno e meno di meno, con conseguenti nuove regole per la moltiplicazione.

Ad esempio, per moltiplicare 4 + di  per 3+ di Bombelli dice:

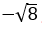
Da qui possiamo trovare le radici di numeri negativi; dalle regole esposte si ha più di meno 2 per più di meno 2 fa – 4, e quindi una radice di – 4 sarà più di meno 2 e l’altra meno di meno 2.

Queste nuove regole e questi nuovi segni diedero origine allo studio dei numeri complessi, partendo dalla traduzione di espressioni come 3 più di meno 2 in 3+2i.