Le equazioni di primo grado nella matematica egizia

Secondo Otto Neugebauer¹, storico della matematica e delle scienze dell’antichità, “La matematica egizia, anche se non ha dato alcun contributo positivo allo sviluppo delle conoscenze matematiche, permette di osservare una fase di sviluppo iniziale delle teorie matematiche, che altrimenti sarebbe rimasta sconosciuta".

Infatti, a differenza di quanto accadde per la matematica babilonese, in alcuni dei grandi papiri matematici egiziani collocabili tra il 1900 e il 1600 a.C. troviamo questioni pratiche riconducibili a problemi matematici risolvibili solo con equazioni di primo grado, cosa che invece non accade per la matematica babilonese.

                                                                      Da Ugo Cassina, "Dalla geometria egiziana alla matematica moderna", Ed. Cremonese, Roma, 1961

Qui ne consideriamo due notevoli esempi.
In primo luogo, osserviamo, nel cosiddetto Papiro di Mosca², datato 1890 a.C., il problema n.19, dove appare per la prima volta, come valore di incognita, il termine "aha", che significa mucchio.
Il problema è il seguente:

Metodo per calcolare un mucchio (1 + 1/2) volte [questo mucchio] con 4 è diventato 10. Quanto èquesto mucchio?
Calcola tu l'eccesso di questo 10 sopra questo 4, è 6. Calcola tu con 1 + 1/2 fino a che trovi 1. Risulta2/3. Pensa tu 2/3 di questo 6. Risulta 4. Ecco, è 4; tu l'hai trovato correttamente. 

che, tradotto in termini moderni, ci porterebbe a cercare di risolvere l'equazione algebrica:
Il papiro suggerisce di procedere con lo stesso metodo che usiamo oggi e che, scritto in termini dell’equazione, dà origine inizialmente a:

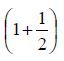
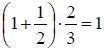
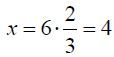A questo punto, il matematico egizio cerca di rendere il coefficiente dell'incognita uguale a 1 e, per far questo, prima determina il numero che moltiplicato per dà appunto 1 - e ottiene , e poi lo moltiplica per il termine noto 6 ottenendo il risultato  .

Tale metodo non è però l'unico usato dagli antichi Egiziani per risolvere le equazioni di primo grado: consideriamo - ed è il secondo caso notevole che vogliamo considerare - il problema n. 25 del Papiro Rhind³  "Una quantità sommata con la sua metà diventa 16".

Oggi, per risolverlo, scriveremmo subito l'equazione: 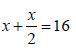per ottenere .

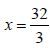Il matematico egizio lo risolve invece in questo modo:

"Conta con 2. Allora (1 + 1/2) di 2 è 3. Quante volte 3 deve essere moltiplicato per dare 16, lo stesso
numero di volte deve essere moltiplicato 2 per dare il numero esatto. Allora dividi 16 con 3. Fa 5 +
1/3. Ora moltiplica 5 + 1/3 per 2. Fa 10 + 2/3. Hai fatto come occorre: la quantità è 10 + 2/3; la sua
metà è 5 + 1/3; la loro somma è 16."

In questo modo, il risultato viene ottenuto applicando un procedimento molto diffuso nell'antichità, detto metodo della falsa posizione, antenato di quel procedimento che oggi chiamiamo metodo del tre semplice. Anziché indicare il valore da trovare con una incognita e operare su questa, la si pone uguale ad un valore vero e proprio, scelto a caso, ma in modo che le operazioni indicate risultino facilmente eseguibili. Una volta compiute le operazioni opportune, se si perviene al risultato richiesto (in questo caso 16), allora il problema è risolto; in caso contrario si stabilisce in che rapporto stanno il risultato richiesto e quello ottenuto a partire dal numero fissato ad arbitrio. Tale rapporto deve sussistere anche tra il numero cercato e quello posto. Per cui il numero cercato è uguale al prodotto del citato rapporto per il numero posto:

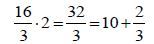e ciò equivale a risolvere la proporzione 2 : 3 = x : 16.

¹ Nato ad Innsbruck, in Austria, nel 1899. Otto Neugebauer studiò dapprima Fisica e Ingegneria elettrica all’’Università di Graz e in seguito Matematica all’Università di Munich. Nel 1922 si trasferì a Göttingen dove insegnò per sette anni.

² E. Bortolotti, La scienza algebrica degli Egizi e dei Babilonesi, Azzaguidi, Bologna 1935

³ Eisenlohr A., Ein Matematisches Handbuch der alten Aegypter (Papyrus Rhind des British Museum). Ubersetzt und erklrt. Leipzig, Hinrich, 1891.