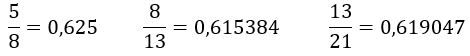L’enigma dei conigli del Fibonacci

Nel 1202, Leonardo Pisano, detto il Fibonacci, con la pubblicazione del suo trattato “Liber Abaci” riuscì a convincere i suoi colleghi europei che il sistema di numerazione decimale, in uso fino ad oggi, era di gran lunga più conveniente di quello romano.

Oltre a questa importante conclusione nella sua opera è presente uno dei più intriganti enigmi matematici della storia, conosciuto con il nome di “Sequenza di Fibonacci”. Analizziamo alcuni aspetti di tale enigma, che sottolineano come la matematica sia essenzialmente uno studio di schemi e di strategie.

L’enigma:

Un tale mise una coppia di conigli, un maschio e una femmina, in una grande gabbia. Quante coppie di conigli verranno generate in quella gabbia in un anno, se ogni mese ogni coppia genera una e solo una nuova coppia ( formata da un maschio e una femmina) che dal secondo mese di vita in poi è fertile? Si assuma che nessuno dei conigli muoia nel corso dell’anno.

Cerchiamo di schematizzare.

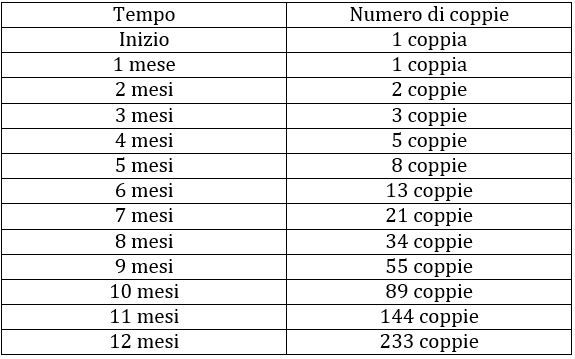
All’inizio nella gabbia si trova solo una coppia di conigli, quella di partenza. Alla fine del primo mese c’è sempre solo una coppia nella gabbia, in quanto una coppia diventa fertile solo “dal secondo mese di vita”. Nel corso del secondo mese, la coppia darà vita alla prima copia di cuccioli; quindi alla fine del secondo mese nella gabbia ci sarà un totale di due coppie - quella di partenza e la prima coppia generata.
Seguendo questo ragionamento alla fine dell’anno via saranno 233 coppie. Ecco un riassunto di tutte le coppie nella gabbia mese dopo mese:

La soluzione dell’enigma, quindi, è che dopo 12 mesi nella gabbia ci saranno 233 coppie. Tale risposta è di per sé poco interessante. Davvero curioso invece è lo schema estratto mettendo semplicemente in sequenza i numeri che indicano le coppie di conigli nella gabbia alla fine di ogni mese: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233

Tale sequenza cela diverse proprietà. Vediamone alcune.

1) Ogni numero è la somma dei due numeri precedenti. Per esempio: 2 = 1+1    3 = 2+1    5 = 3+2   8 = 5+3    13 = 8+5

Questa proprietà ci permette di estendere la sequenza all’infinito; infatti per scoprire quale numero ci sarà dopo il 233, basta sommare 233 e 144 ed ottenere 377, e così via.

In generale: F_n = F _n-1 + F_n-2

2) Prendiamo in considerazione il rapporto fra due numeri consecutivi della sequenza, per esempio:

Tale rapporto tende al numero decimale illimitato: 0,6180339....., che corrisponde proprio al valore della Sezione Aurea, un rapporto scoperto dai Greci e riconosciuto come uno standard per il giudizio estetico.

3) La sequenza che si ottiene elencando le differenze fra due numeri di Fibonacci consecutivi dà vita ancora alla sequenza originale: 2-1 = 1  3-2 = 1  5-3 = 2  8-5 = 3  13-8 = 5   21-13 = 8 .....

Altre proprietà le lascio verificare a voi.

• La somma dei quadrati di due numeri di Fibonacci consecutivi è un numero di Fibonacci.
• Il terzo numero è 2, e ogni terzo numero dopo il 2 è un multiplo di 2; il quarto numero è 3, e ogni quarto numero dopo il 3 è multiplo di 3....e così via.