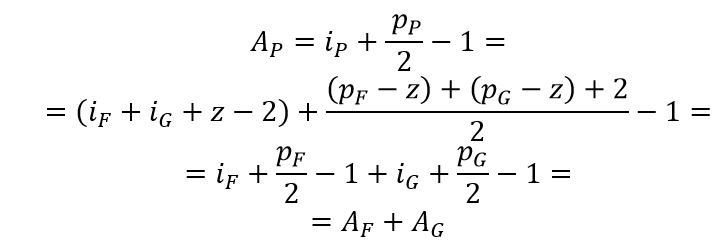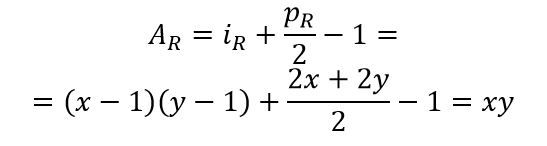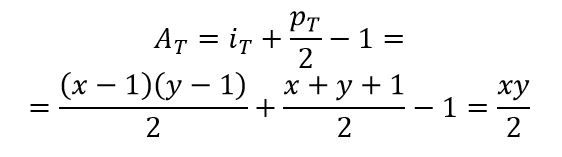Il Teorema di Pick
A volte capita che non è possibile utilizzare le comode e familiari formule per il calcolo delle aree delle figure geometriche.
In questi casi può essere utile conoscere il Teorema di Pick che permette di calcolare l’area di poligoni disegnati sulla carta a quadretti, aventi i vertici su di essa.
Consideriamo un foglio di carta a quadretti e un poligono disegnato su di esso, in modo tal che i vertici del poligono coincidano con i nodi della quadrettatura.
Il teorema afferma che detti:
• i il numero di nodi interni al poligono
• p il numero di nodi appartenenti al perimetro del poligono (vertici compresi)
l’area A del poligono può essere calcolata tramite la formula:
Dimostrazione
La dimostrazione del teorema si sviluppa in tre fasi:
• dimostrare che la formula è additiva;
• dimostrare che la formula vale per rettangoli;
• dimostrare che la formula vale per triangoli rettangoli che non hanno punti della quadrettatura sull’ipotenusa a parte gli estremi.
Fase 1
Consideriamo un poligono P e tracciamo una sua diagonale dividendolo in altri due poligoni F e G i cui lati di contatto condividono z punti della quadrettatura e applichiamo a P la formula.
Fase 2
Consideriamo ora un rettangolo R di lati x e y sulla quadrettatura e applichiamo a R la formula:
Fase 3
Consideriamo infine un triangolo T di cateti x e y la cui ipotenusa non contiene punti della quadrettatura sull’ipotenusa a parte gli estremi. Applichiamo la formula:
Queste tre fasi concludono la dimostrazione in quanto ogni poligono può essere diviso in triangoli tracciando tutte le diagonali che escono da uno stesso vertice e ogni triangolo si può dividere in rettangoli e triangoli rettangoli senza punti della quadrettatura sull’ipotenusa.