I primi di mersenne

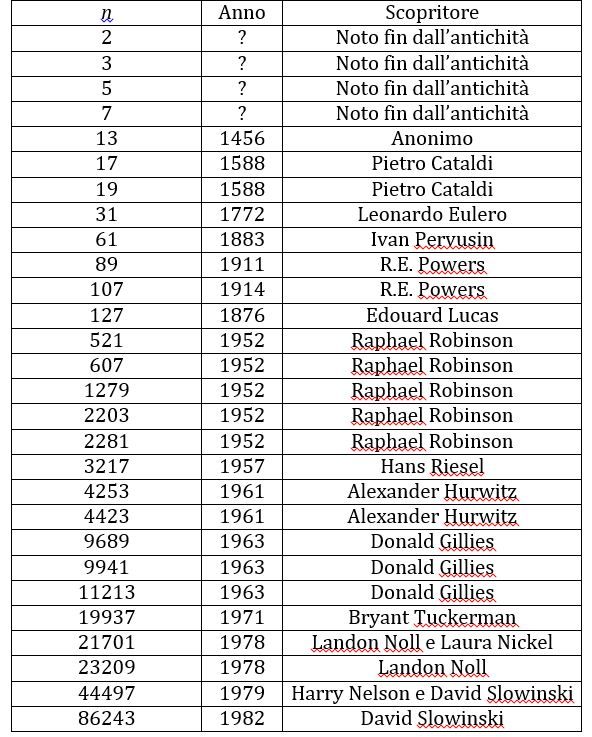
Un numero di Mersenne è un numero della forma 2ⁿ-1; mentre un primo di Mersenne è un numero di Mersenne che sia anche un numero primo. E’ immediato dimostrare che in questo caso anche l’esponente n deve essere un numero primo; infatti per i primi numeri primi, n = 2, 3, 5 e 7, i corrispondenti numeri di Mersenne sono tutti primi: 3, 7, 31 e 127.
L’interesse per i numeri di Mersenne risale a molto tempo fa, e inizialmente si credeva che fossero primi per ogni valore primo di n.
Ma nel 1536 Hudalricus Regius dimostrò che questo è falso, osservando che 2¹¹-1=2047=23 × 89 .
Nel 1603 Pietro Cataldi notò che 2¹⁷-1 e 2¹⁹-1 sono primi e affermò che anche per n = 23, 29, 31 e 37 si ottengono numeri primi.
Fermat mostrò che Cataldi sbagliava per n = 23 e n = 37, ed Eulero confutò la sua tesi riguardo ad n = 29.

Nel suo libro del 1644 intitolato Cogitata Physico-Mathematica, il monaco francese Marin Marsenne affermò che 2ⁿ-1 è primo quando n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 e 257, e per nessuno altro valore prima di 257. Ovviamente, usando i metodi disponibili all’epoca non può aver verificato molti di questi numeri, e quindi le sue asserzioni erano per lo più supposizioni, ma il suo nome rimase legato a questo problema.
Con metodi più moderni, alcuni matematici del XIX e XX secolo hanno dimostrato che Mersenne aveva sbagliato ad inserire il 67 e il 257 e aveva omesso il 61, 89, e 107.

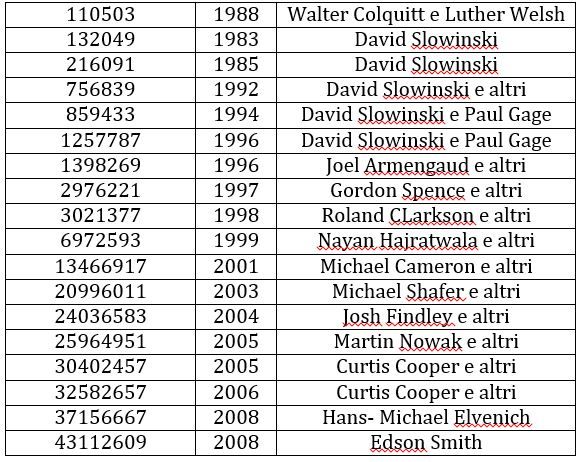
Nel corso degli anni sono stati individuati nuovi primi di Mersenne sempre più grandi, anche attraverso l’uso di potenti computer, e nel 2008 la lista ne comprendeva 46.

 Per informazioni maggiori e aggiornate, si può visitare il sito www.mersenne.org