Algebra

“Algebra” è una delle parole più nominate nelle nostre scuole superiori e anche chi ha concluso gli studi da qualche anno senza dubbio la ricorda, ma siamo sicuri di sapere che cosa significa veramente? Proviamo a scoprirlo insieme. In origine, con la parola "Algebra" si intese lo studio sistematico di regole generali pensate per trovare le soluzioni di equazioni numeriche. In seguito il termine indicò, e indica tuttora, anche lo studio delle cosiddette “strutture algebriche”, cioè di insiemi nei quali - o a partire dai quali - sono definite delle “operazioni” e delle corrispondenze che si possono stabilire tra di essi.

Il termine “algebra” è relativamente recente: è di origine araba e deriva dal titolo dell'opera di Mohammed ibn Musa al Khuwarizmi¹(IX sec.): Al-giabr wa-l-muqabala. Questo titolo si può tradurre con "trasporto e riduzione" per indicare sia l'operazione di trasporto, che viene solitamente compiuta nelle equazioni algebriche per portare opportunamente un termine da una parte all’atra del segno di uguaglianza, sia l’azione di sommare e sottrarre tra loro termini simili.

Se ci domandiamo che tipo di svolgimento ha avuto la storia di questa disciplina, possiamo, per iniziare, provare a scandirne lo sviluppo formale in alcuni stadi fondamentali:

Primo stadio: la nascita del cosiddetto "spirito algebrico"
Si cominciano a manipolare i dati di un problema alla ricerca di valori che non sono noti, ma che sono coinvolti in procedimenti i cui i risultati finali sono conosciuti.
In questo stadio si ha bisogno del concetto e del segno di uguale: "Forse il più importante di tutti i simboli - scrive Joseph Needham²- quello che rende possibili le equazioni, era il segno = dell'uguaglianza."

 Secondo stadio: la prima generalizzazione dei procedimenti

Ripetendo più volte lo stesso procedimento in situazioni diverse, si arriva in modo naturale ad una sua generalizzazione, passando anche attraverso l’introduzione di termini tecnici che assumono significati diversi rispetto a quelli della loro origine. Per esempio, il termine "rettangolo" può essere inteso come "prodotto di due numeri incogniti" e termini come "quadrato” o come “cubo" possono assumere un significato esclusivamente numerico.

 Terzo stadio: i simboli per le incognite

Nascono segni particolari per indicare le incognite, trattate come i numeri, in modo da operare tra incognite e termini noti alla stessa maniera.

 Quarto stadio: le espressioni con le lettere

Compaiono le prime espressioni letterali anche per le quantità considerate note, così da rendere assolutamente generali i procedimenti indicati. Si hanno pertanto espressioni algebriche che esprimono identità e formule risolutive come quelle che oggi scriviamo nella forma:

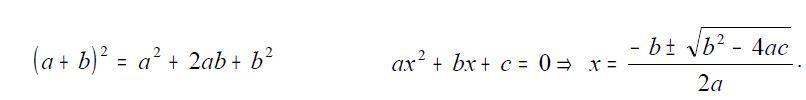
Quinto stadio: le soluzioni negative o complesse

Si amplia l'estensione del campo numerico in cui (sono dati i coefficienti delle equazioni e – soprattutto - in cui) si possono determinare le soluzioni di un’equazione. Ciò porta a trovare tutte le soluzioni di un'equazione numerica indipendentemente dal loro significato nel contesto del problema (soluzioni negative o, addirittura, complesse). Tale estensione si compie sia per problemi geometrici che algebrici (e a scuola la incontriamo, per esempio, quando incominciamo a togliere le solite limitazioni al segno del discriminante nella risoluzione delle equazioni di secondo grado).

Sesto stadio: la formalizzazione degli assiomi

Si ha infine un ulteriore sviluppo quando le varie operazioni che si compiono nei passaggi algebrici vengono assiomatizzate, quando si stabiliscono, quindi, gli assiomi dell'uguaglianza in modo da poter passare da un'equazione ad un'altra equivalente, estendendo quelle "nozioni comuni" che si trovano nel primo libro degli Elementi di Euclide.

Anche da queste poche righe risulta evidente che questa branca della matematica ha avuto una sua propria, lunga e ricca, evoluzione: ciò che studiamo noi oggi è il frutto di secoli di prove e ricerche. E l’essere riusciti a superare l’ostacolo della traduzione in simboli astratti di ciò che prima veniva espresso solo a parole ci sembra che sia stato “il” passo decisivo che ha portato alla nascita di uno strumento di grande utilità. 

¹ L’immagine è tratta da http://www.dti.unimi.it/citrini/MD/equazioni/alkhuwarizmi.htm

² Needham Joseph, Scienza e civiltà in Cina, Vol.1, Torino Einaudi, 1981