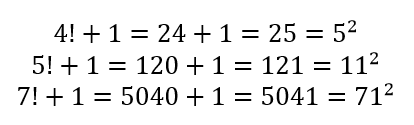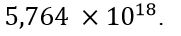Quattro problemi... ancora da dimostrare

A volte, si ha l’impressione che la matematica sia una disciplina senza più domande, invece i matematici sono in continua ricerca. Ci sono congetture ancora in attesa di una dimostrazione… vediamone alcune.
Il problema di Brocard
Per qualsiasi intero n, il suo fattoriale n! è il prodotto:
In riferimento a tale argomento, tra il 1876 e il 1885, Henri Brocard osservò che:
cioè tutti i risultati sono quadrati perfetti.
Non riuscendo a verificare la proprietà per altri fattoriali, si chiese se fosse sempre verificabile.
Indipendentemente, nel 1913, tale congettura rientrò anche negli studi del matematico indiano autodidatta Srinivasa Ramanujan. Nel 2000 altri due matematici mostrarono la non esistenza di ulteriori soluzioni per fattoriali fino a un miliardo.
Numeri perfetti dispari
I numeri perfetti sono quei numeri uguali alla somma di tutti i suoi divisori propri, eccetto se stesso, per esempio:
6 = 1 + 2 + 3
28 = 1 + 2 + 4 + 7 + 14
Euclide dimostrò che se 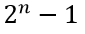
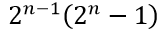
I primi di questa forma, come già detto in un’altra occasione, sono detti primi di Mersenne e se ne conoscono attualmente 48.
Eulero dimostrò che tutti i numeri perfetti pari devono avere questa forma, mentre ancora nessuno ha trovato un numero perfetto dispari, né ha dimostrato la loro non esistenza. Solo il matematico Pomerance ha provato a mostrarlo con un ragionamento non rigoroso.
La congettura di Collatz
Consideriamo un numero intero. Se è pari, dividiamolo per 2; se è dispari, moltiplichiamo per 3 e sommiamo 1 e iteriamo il procedimento. Cosa succede?
Per esempio, se partiamo da 12 i numeri che troviamo sono:
12→6→3→10→5→16→8→4→2→1
e la sequenza 4→2→1 si ripete all’infinito.
Il matematico Lothar Collatz, nel 1937, formulò la tesi, senza dimostrarla, che da qualunque numero si parta, si arriva sempre alla stessa sequenza. Ad oggi, è stata solo verificata, attraverso un computer, per tutti i numeri inziali fino a:
La congettura del corridore solitario
Questo particolare nome fu coniato da Luis Goddyn nel 1998 per una congettura formulata da Jorg Wills nel 1967.
Supponiamo che n corridori percorrano una pista circolare di lunghezza unitaria a velocità uniformi, tutte diverse. È vero che ognuno dei corridori in qualche momento sarà solitario, cioè ad una distanza 
La risposta è ovviamente positiva per i diversi corridori in diversi momenti, ma la congettura è che sia sempre positiva.
Ad oggi è stata dimostrata per n = 4, 5, 6, e 7